Kun juhlia siirretään vuodella eteenpäin jo toista vuotta, joutuu tyytymään sellaisista haaveilemiseen. Diletantti selvitti, miten sinunkin seuraavassa juhlatilaisuudessasi kakun leikkaus vieraiden nautittavaksi sujuu täydellisesti. Ja kun sanomme täydellisesti, tarkoitamme tietenkin matemaattisessa mielessä täydellisesti.

Mutta millainen oikeastaan on täydellisen onnistunut kakunleikkaus? Tieteellisessä kirjallisuudessa kysymystä on pohdittu jo pitkään useista eri näkö- ja leikkuukulmista. Nature-tiedelehdessä on esitetty jo vuonna 1908 menetelmä, jolla kakun leikkuupinta ja siten kakun kuivuva pinta-ala eliminoidaan sitä säilytettäessä. Tätä aihepiiriä käsittelimme jo aiemmin lantun leikkauksien yhteydessä.

Kakkua ei muutenkaan soisi jäävän täydellisistä juhlista säilytettäväksi asti, vaan sen sijaan haluamme jakaa sen niille lukemattomille vieraille, jotka rajoitusten poistuttua saapuvat matemaattisille kahvikesteillemme. Tässäkin tilanteessa paras mahdollinen tapa jakaa kakkua riippuu tavoitteista: esittelemme alkuun tapoja maksimoida kakkupalojen määrä tai tuottaa tasakokoisia paloja. Testasimme myös useampaa kakunjakoalgoritmia, joita noudattamalla jokainen juhlavieras voi saada yli oman osansa kakusta!

Kakkujen eri abstraktiotasoja: vasemmalta lukien kakku, kolmiulotteinen kakun malli, Diletantin kaksiulotteinen kakun malli ja matemaatikon yksiulotteinen kakku.

Todellinen kakku on tietenkin varsin hankala mallintaa matemaattisesti, joten yksinkertaisuuden vuoksi oletamme tässä jutussa, että kakut ovat ympyrälieriöiden muotoisia. Lisäksi oletamme, että kakkuja voidaan käsitellä kaksiulotteisina: emme siis salli vieraiden keräävän mukaansa pelkkää kuorrutetta. Diletantin kokemusten mukaan kakut ovat luonnossakin varsin usein ympyränmuotoisia, ja vain kirsikat kakun päältä poimivia vieraita katsotaan muutenkin pahalla. Jos kakusta sallitaan leikattavan vain sektoreita, voidaan matemaatikon kakkua kuvata yksiulotteisena: kakkupalan kattama osuus reunasta määrittelee yksikäsitteisesti, mitkä osat kakun sisuksista kuuluvat palaan.

Palojen määrän maksimointi

Kakun leikkaaminen mahdollisimman monen palan tuottamiseksi.

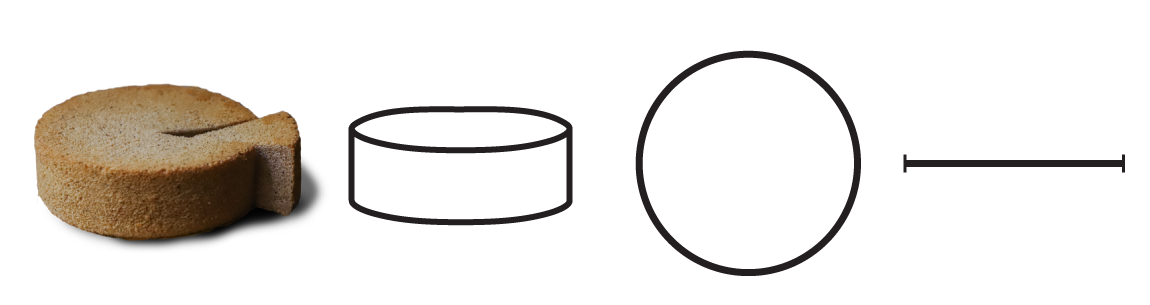
Monet kakut ovat oletettavissa homogeenisiksi, kuten kuvan suklaakakku, jonka reunoilla ei ole kuorrutetta. Kiireinen pitojen emäntä haluaisi leikata kakun mahdollisimman moneen osaan mahdollisimman nopeasti. Maksimimäärä paloja saavutetaankin, kun jokainen uusi veitsenviilto risteää kaikkien aiempien viiltojen kanssa, mutta missään pisteessä ei ole kolmen viillon risteystä. Kahdella leikkauksella saavutetaan neljä palaa, kolmella seitsemän, neljällä yksitoista, mutta viidennellä mössöä. Matemaattisesti paloja tulisi saavuttaa n:llä leikkauksella 1 + (n+1)*n/2, mutta ohjeessa kehotetaan mössön välttämiseksi suurentamaan kakkua ja sen jälkeen pienentämään koko avaruutta, jotta kaikki viillot lopulta risteävät kakun sisällä. Ei kovin käytännöllistä.

Tasakokoisuuden tavoittelu tasalaatuisella kakulla

Tasakokoisten kakkupalojen leikkaamista sektoreina, "suorakulmioina" tai kolmioina.

Tasakokoisten kakkupalojen saavuttamiseksi perinteinen ratkaisu on leikata kakku sektoreiksi, mutta niistäkin syntyy harmittavan ohuita hyvin äkkiä. Internetin mukaan kakusta pitäisi saada tasakokoisia paloja leikkaamalla kakku ensin puoliksi, ja sen jälkeen näennäisen suorakulmaisia paloja kakun puolikkaasta. Mutta miten ihmeessä tällaisten puoliympyräsegmenttien pinta-alan integrointi muka olisi helpompaa kuin kulman jakaminen osiin? Helppo tapa tuottaa tasakokoisia paloja on kuitenkin löydettävissä oikeanpuolimmaisen kuvan mukaisella kolmiohilalla, joka tuottaisi standardikokoisesta (halkaisija 24 cm) kakusta siististi 24 samanlaista kakkupalaa reunapalojen vähäisen hävikin hinnalla.

kakku, jonka päällä on kirsikoita

Kaikki kakut eivät ole samanlaisia eivätkä kaikki kakkujen päällysteet yhtä herkullisia.

Monimutkaisempaan kakunjakoprobleemaan päästään epähomogeenisten kakkujen kanssa. Kuvan esimerkkikakun kuorrutteen alta löytyy kaikkialta samaa kakkupohjaa, mutta hiukan hajamielinen kondiittorimme on laittanut koristeeksi sekä tuoreita ananaskirsikoita, säilöttyjä cocktail-kirsikoita että kalamata-oliiveja. Lisäksi kinuski on jakautunut silminnähtävän epätasaisesti kakun reunoille. Juhlavieraiden eli tässä tapauksessa toimituksen testiryhmän mieltymysten voidaan perustellusti olettaa eroavan näiden eri "kirsikoiden" suhteen.

Kahdella hengellä tällaisenkin kakun jakaminen on helppoa: toinen jakaa kakun mielestään tasavertaisiin puolikkaisiin, ja toinen valitsee mieluisemman puolikkaan. Kakun leikkaaja saa itse siis mielestään tasan puolet kakusta, ja valitsija saattaa jopa saada valittua itselleen mieluisimman puoliskon. Kumpikaan kokee saaneensa ainakin oman osansa eikä ole kateellinen toisen palasta: jako on siis näillä mittareilla reilu. (Mahdollisia reiluuden mittareita on toki muitakin). 

Vaikka tämä jako on reilu, se ei kuitenkaan välttämättä ole paras mahdollinen. Jos kakunleikkaaja sattuisi vihaamaan cocktail-kirsikoita, voisi hän jakaa ne tasan palojen kesken tuottaakseen keskenään yhtä hyvät palat, vaikka valitsija pitäisi kirsikoista kovasti! Olisi molempien mielestä parempi, jos kirsikat päätyisivät niiden ystävälle. Tässä mielessä optimaalisen kakunleikkauksen tuottaminen on kuitenkin merkittävästi monimutkaisempaa kuin reilun jaon.

Useamman vieraan tilanteessa ei kuitenkaan ole aivan ilmeistä, miten kakku jaettaisiin niin, että kaikki kokisivat saaneensa edes sen oman osansa. Onneksi tiede tuottaa käyttökelpoista tietoa maalaisjärjen jatkoksi tässäkin tilanteessa, ja varsin käyttökelpoisia algoritmeja kakun oikeasuhtaiseen jakoon löytyy useita. Diletantti kokeili näistä käytännössä kahta.

Tällä kertaa rajoituimme yksinkertaisuuden vuoksi tilanteeseen, jossa kakusta saa leikata vain sektoreita. Oletamme myös, että niin itse kakkua, oliiveja kuin kirsikoitakin on mahdollista leikata mielivaltaisen pieniin osiin. Ennen kakun leikkaamisen aloittamista kaikilla pelaajilla on mahdollisuus tutustua kakun päällisiin ja muodostaa oma mielipiteensä kakun eri osioista. Tärkeä oletus on myös se, että pelaajat ylipäänsä haluavat kakkua, vaikka ehkä haluaisivatkin välttää oliiveja sisältäviä palasia.  (Matemaattisempaa formulointia kaipaaville lukijoille suosittelemme Toronton yliopiston luentokalvoja.)

Viimeisen pienentäjän menetelmä

Pienennettyjä palasia ja viimeisen pienentäjän menetelmän tuottamia kakkupaloja.

Viimeisen pienentäjän menetelmässä valitaan vaikkapa nuorin pelaajista aloittamaan kakun leikkaaminen. Aloittaja leikkaa itselleen mieluisan osuuden kakusta. Seuraava pelaaja voi joko pienentää tätä edellisen pelaajan leikkaamaa kakkupalaa tai passata. Näin jatketaan mahdollisesti useiden kierrosten ajan, kunnes kaikki pelaajat ovat passanneet. Se, joka on viimeksi koskenut kakkupalaan, saa sen itselleen. Tämän jälkeen algoritmi aloitetaan alusta jäljellejääneiden pelaajien kesken jäljelläolevalla kakkuosuudella, johon siis sisältyvät edellisestä palasesta mahdollisesti pois jätetyt palaset.

Kakkupalaa kannattaa siis pienentää vain, jos on valmis kelpuuttamaan jäljellekin jääneen kakkupalan itselleen. Näin tietysti kannattaa tehdä vain siinä tapauksessa, että kokee saavansa vähintäänkin oman osansa, eikä paloja kannata pienentää muita pelaajia kiusatakseen. Syntyvä kakun jako on siis tässä mielessä reilu. Koekierroksellamme kakku jakaantui melko tasakokoisiin paloihin, mutta ei samannäköisiin sellaisiin. Todellisesta kakustamme syntyy erittäin epäkuvauksellista kakkumössöä, kun paloja leikataan kerta kerralta pienemmäksi, joka vähensi niiden koettua nautinnollisuutta.

Even-Paz -protokolla

Viimeisen pienentäjän menetelmä saattaa vaatia melko monta leikkuukierrosta. Tehokkaampi algoritmi on rekursiivinen Even-Paz -protokolla. Tässä kaikki pelaajat asettavat merkin siihen kohtaan, mistä kakku tulisi puolittaa, jotta kumpikin pala olisi yhtä hyvä. Kakku jaetaan kahtia keskimmäisten merkkien kohdalta: esimerkiksi kahdeksan pelaajan kakulla neljännen ja viidennen merkin välistä. Leikkauskohdan vasemmalle puolelle merkkinsä jättäneet pelaajat toistavat saman algoritmin vasemmalla kakkupalalla, ja oikean kakkupalan pelaajat tekevät samoin. Tätä toistetaan, kunnes jäljelle jää yhden pelaajan kokoisia paloja.

Kakun leikkaamista eri pelaajien asettamien merkkien välistä.

Diletantin käytännön kokeessa todettiin, että menetelmän laskennallinen tehokkuus tuotti myös käytännössä huomattavasti siistimpiä kakkupaloja kuin viimeisen pienentäjän menetelmä. Osansa tähän saattoi tosin olla myös apuvälineinä käytetyillä cocktail-tikuilla. Toisaalta toisen kakun kohdalla kakkuhalutkin olivat jo vähentyneet.

Lopuksi

Ylläolevilla kakkujakoalgoritmeilla saadaan teoreettisesti jako, joissa kukin kokee saaneensa vähintäänkin oman osansa kakusta. Nämä algoritmit eivät kuitenkaan takaa, että kateudelta vältyttäisiin: jonkun muun pala voisi olla vielä mieluisampi kuin itselle päätynyt pala. Kolmelle hengelle kateuden välttävä algoritmi on esitetty englanninkielisessä Youtube-videossa, mutta useammille kakunsyöjille tällainen jako muuttuu jo hyvin monimutkaiseksi. Kakkujen reilu jakaminen onkin aktiivinen tutkimusaihe, jonka sovelluksia ovat esimerkiksi jonkin maa-alueen jakaminen eri intressiryhmille. Ongelma muuttuu entistäkin mutkikkaammaksi, jos pelaajat saattavat valehdella mieltymyksistään.

Aivan konkreettistenkin kakkujen reilun jakamisen kannalta ongelmallisimmaksi oletukseksi osoittautui se, että ihmiset tietäisivät, mitä haluavat. Miten muka tietäisi ennen kakun syömistä, kuinka montaa cocktail-kirsikkaa yksi ananaskirsikka vastaa? Lisäksi todellisessa kakunsyöntitilanteessa ensimmäistä kakkupalaa vaille jääminen olisi paljon suurempi menetys kuin se, että santsaamaan ei pääse. Kakunnälkä siis useimmiten vähenee syödessä, ja koko kakun syöminen todennäköisesti kaduttaisi. Algoritmit eivät huomioi tätä, vaan olettavat, että kaikki haluaisivat mieluiten koko kakun itselleen. Kakun matemaattinen jakaminen oli jopa yllättävänkin helppoa ja ainakin sopivassa seurassa epäilemättä hauska seuraleikki, mutta muistutti myös taas kerran, miten tärkeää on tarkistaa, toteutuvatko matemaattisen mallin oletukset todellisuudessakin.

Ja viimeiseksi: kyllä, oliivit kinuskikakussa olivat kokeilemisen arvoinen yhdistelmä.

---